Berkeley Institute for Theoretical Science
Bespoke research in the fields of Quantum Machine Learning, Non-equilibrium thermodynamics, and the Physics of Information.
The Dynamics Of Disorder
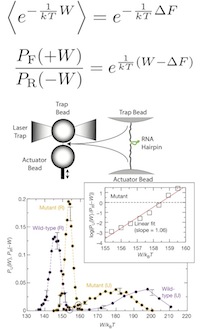The fundamental dynamical laws of physics are time reversal symmetric. The only fundamental theory that picks out a preferred direction of time is the second law of thermodynamics, which asserts that the entropy of the Universe increases as time flows towards the future.
When the dissipation, or the total increase in entropy, is large, the orientation of time’s arrow is self-evident. If we watch a movie in which shards of pottery jump off the floor, assemble themselves into a cup, and land on a table, then clearly someone has threaded the film through the projector backwards. On the other hand, if the dissipation is microscopic, then the distinction between past and future becomes nebulous. If we repeat the same experiment many times, the entropy might increase or decrease on different occasions. Only the average dissipation must be positive.
This tension between the time-symmetry of the microscopic dynamical laws and the inexorable increase of macroscopic entropy leads to a rich dynamics of disorder at the nanoscale, that is particularly pertinent to driven, molecule scale machines operating away from thermodynamic equilibrium. I uncovered one of the key relations, the Work Fluctuation Theorem, and continue to explore the consequences of fluctuation theorems for nanoscale thermodynamics.
-
Near-equilibrium measurements of nonequilibrium free energy, PRL (2012)
-
On thermodynamic and microscopic reversibility, J. Stat. Mech. (2011)
-
Work distribution for the adiabatic compression of a dilute and interacting classical gas, (2007)
-
Experimental test of Hatano and Sasas nonequilibrium steady-state equality, PNAS (2004)
-
Path ensemble averages in systems driven far from equilibrium, PRE (2000)
Thermodynamics of Molecular Computation
Living systems compute, on a variety of length- and time-scales, future expectations based on their prior experience. Most biological computation is fundamentally a nonequilibrium process, because a preponderance of biological machinery in its natural operation is driven far from thermodynamic equilibrium.
A system responding to a stochastic driving signal can be interpreted as computing, by means of its dynamics, an implicit model of the environmental variables. The system’s state retains information about past environmental fluctuations, and a fraction of this information is predictive of future ones.
There are profound connections between the effective use of information and efficient thermodynamic operation: any system constructed to keep memory about its environment and to operate with maximal energetic efficiency has to be predictive.
The Geometry of Thermodynamic Control
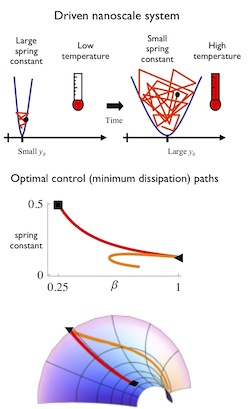A fundamental problem in modern thermodynamics is how a molecular scale machine can perform useful work without excessive dissipation, while operating away from thermal equilibrium.
Concretely, we can ask how should we perform a finite-time transformation of a microscopic system (in this example, a single particle) so as to minimize the dissipation. If we wish to go from a strongly trapped particle at low temperature to a weak trap at high temperature, should we increase temperature first, then reduced the trap strength, or vice versa, or something in between?
The lower part of the figure shows that optimal protocols appear complicated, even for simple systems. But with a change of coordinates we can see that the minimum dissipation protocols are straight lines (technically geodesics) on a curved surface. Thermodynamic control near-equilibrium has a Riemannian geometry (similar to general relativity), and we can use this mathematics to design and analyze molecular machines.
Quantum Dynamics and Control
At the molecular scale, the flow of energy and information can be strongly influences by quantum mechanics. The photosynthetic reaction center, for instance, appears to use quantum coherence to control and corral the large energy fluxes through the system.
I’ve recently extended fluctuation theorems to open quantum system with dissipative dynamics. Work is not directly an observable in quantum dynamics, and care is needed to obtain physically meaningful insights.
Measuring Information
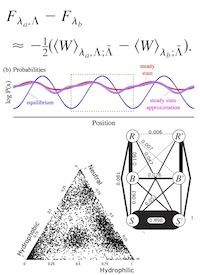Measuring entropy and other information measures is tricky for small systems where we cannot rely on the precepts of equilibrium thermodynamics. We have recently derived a simple near-equilibrium approximation for the relative entropy between two thermodynamic systems, which corresponds to a nonequilibrium free energy. I’ve also studied experimental and computational measurements of a variety of information divergences, that quantify various properties of the system, such as the breaking of time-symmetry.
-
Near-equilibrium measurements of nonequilibrium free energy (2012)
-
Measures of trajectory ensemble disparity in nonequilibrium statistical dynamics,
A distinct, but related problem is the measurement of entropy from small data sets. I’ve developed statistical methods to extract reliable measures of entropy from small sample sizes, and used these entropies to measure the correlations in proteins and DNA sequences, quantifying evolutionary conservation and the interactions between sequence and structure.
Computational Simulations and Statistical Dynamics
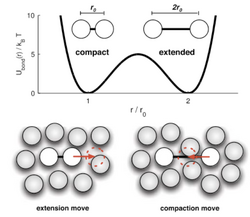Computer simulations are a powerful tool for studying the properties of matter, and I’ve studied various techniques for making simulations faster, more efficient, less biased, and more informative.
Interestingly, ideas from nonequilibrium thermodynamics can often be fruitfully applied directly to computer simulation methods themselves (rather than the subject of the simulation). For instance, simulations of Langevin dynamics can be viewed as a driven, nonequilibrium process, where the driving originates from the necessary discretion of time due to implementation on a digital computer. In another example, a wide range of advanced biased Monte Carlo sampling techniques can be unified under a general scheme of Nonequilibrium Candidate Monte Carlo.
- Using nonequilibrium fluctuation theorems to understand and correct errors in equilibrium and nonequilibrium discrete Langevin dynamics (2013)
- Nonequilibrium candidate Monte Carlo, PNAS (2011)
- Efficient transition path sampling for nonequilibrium stochastic dynamics (2001)
Elegant visualizations of biological information
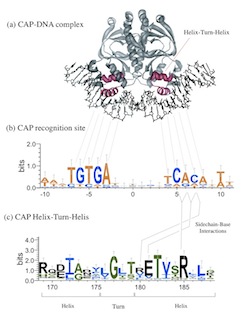I develop, maintain, extend, and support
WebLogo, a web-based application for generating sequence logos. These are small information graphics that clearly present complex patterns of conservation within biological DNA, RNA and protein sequences.
WebLogo employs a sophisticated Bayesian statistical analyses of sequence information to extract reliable measures of entropy from small sample sizes.
WebLogo: A sequence logo generator, Genome Research (2004)
Distributions of Probability
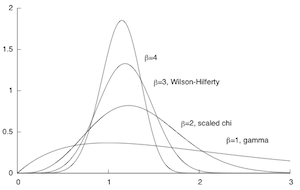In a desperate attempt to preserve my own sanity, I’ve spent some time surveying and categorizing the vast numbers of probability distributions used to describe a single, continuous, unimodal, univariate random variable. There’s much more structure and organization to this menagerie than is commonly appreciated.
The Nature of Time
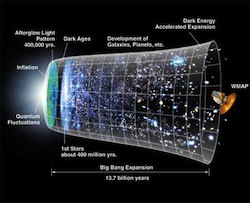In our everyday lives we have the sense that time flows inexorably from the past into the future; that time has a definite direction; and that the arrow of time points towards a future of greater entropy and disorder. But in the microscopic world of atoms and molecules the direction of time is indeterminate and ambiguous.