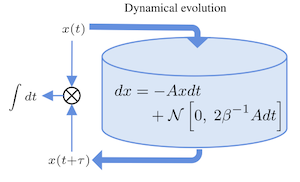
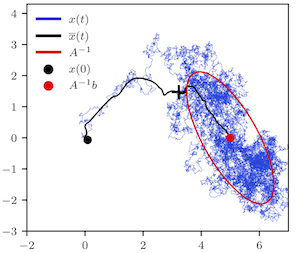
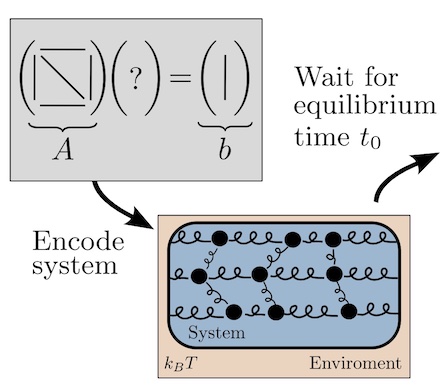
Article: Scaling laws governing stochastic growth and division of single bacterial cells

Srividya Iyer-Biswas, Charles S. Wright, Jonathan T. Henry, Klevin Lo, Stanislav Burov, Yihan Lin, Gavin E. Crooks, Sean Crosson, Aaron R. Dinner, Norbert F. Scherer, Proc. Natl. Acad. Sci. U.S.A. (2014)

[ Full text | Journal | arXiv ]

This is the experimental paper that logically (but, alas, not chronologically) precedes the companion theory paper.

Abstract

Uncovering the quantitative laws that govern the growth and division of single cells remains a major challenge. Using a unique combination of technologies that yields unprecedented statistical precision, we find that the sizes of individual Caulobacter crescentus cells increase exponentially in time. We also establish that they divide upon reaching a critical multiple (≈1.8) of their initial sizes, rather than an absolute size. We show that when the temperature is varied, the growth and division timescales scale proportionally with each other over the physiological temperature range. Strikingly, the cell-size and division-time distributions can both be rescaled by their mean values such that the condition-specific distributions collapse to universal curves. We account for these observations with a minimal stochastic model that is based on an autocatalytic cycle. It predicts the scalings, as well as specific functional forms for the universal curves. Our experimental and theoretical analysis reveals a simple physical principle governing these complex biological processes: a single temperature-dependent scale of cellular time governs the stochastic dynamics of growth and division in balanced growth conditions.