Preprint: Thermodynamic Linear Algebra
Maxwell Aifer, Kaelan Donatella, Max Hunter Gordon, Thomas Ahle, Daniel Simpson, Gavin E. Crooks, Patrick J. Coles
arXiv:2308.05660
Abstract
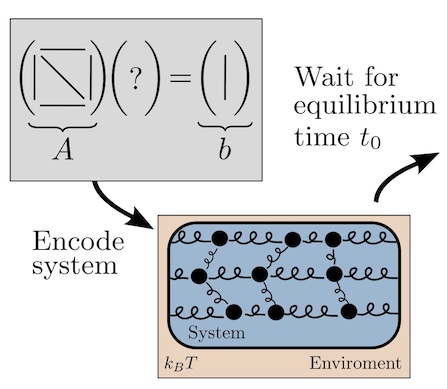 Linear algebraic primitives are at the core of many modern algorithms in engineering, science, and machine learning. Hence, accelerating these primitives with novel computing hardware would have tremendous economic impact. Quantum computing has been proposed for this purpose, although the resource requirements are far beyond current technological capabilities, so this approach remains long-term in timescale. Here we consider an alternative physics-based computing paradigm based on classical thermodynamics, to provide a near-term approach to accelerating linear algebra.
At first sight, thermodynamics and linear algebra seem to be unrelated fields. In this work, we connect solving linear algebra problems to sampling from the thermodynamic equilibrium distribution of a system of coupled harmonic oscillators. We present simple thermodynamic algorithms for (1) solving linear systems of equations, (2) computing matrix inverses, (3) computing matrix determinants, and (4) solving Lyapunov equations. Under reasonable assumptions, we rigorously establish asymptotic speedups for our algorithms, relative to digital methods, that scale linearly in matrix dimension. Our algorithms exploit thermodynamic principles like ergodicity, entropy, and equilibration, highlighting the deep connection between these two seemingly distinct fields, and opening up algebraic applications for thermodynamic computing hardware.
Linear algebraic primitives are at the core of many modern algorithms in engineering, science, and machine learning. Hence, accelerating these primitives with novel computing hardware would have tremendous economic impact. Quantum computing has been proposed for this purpose, although the resource requirements are far beyond current technological capabilities, so this approach remains long-term in timescale. Here we consider an alternative physics-based computing paradigm based on classical thermodynamics, to provide a near-term approach to accelerating linear algebra.
At first sight, thermodynamics and linear algebra seem to be unrelated fields. In this work, we connect solving linear algebra problems to sampling from the thermodynamic equilibrium distribution of a system of coupled harmonic oscillators. We present simple thermodynamic algorithms for (1) solving linear systems of equations, (2) computing matrix inverses, (3) computing matrix determinants, and (4) solving Lyapunov equations. Under reasonable assumptions, we rigorously establish asymptotic speedups for our algorithms, relative to digital methods, that scale linearly in matrix dimension. Our algorithms exploit thermodynamic principles like ergodicity, entropy, and equilibration, highlighting the deep connection between these two seemingly distinct fields, and opening up algebraic applications for thermodynamic computing hardware.


