Article: Using nonequilibrium fluctuation theorems to understand and correct errors in equilibrium and nonequilibrium discrete Langevin dynamics
David A. Sivak, John D. Chodera, Gavin E. Crooks, Phys. Rev. X 3, 011007 (2013)
This paper originated when David was running some precision simulations of driven nonequilibrium systems using Langevin dynamics. We knew the exact answer, but he kept getting systematic errors. Turns out that Langevin integrators don’t simulate equilibrium systems! There is an extra driving term that originates from the discretization of time. After much study, we have pulled together a lot of different papers from the literature, to explain in terms of nonequilibrium thermodynamics why this happens, and how to compensate.
Abstract
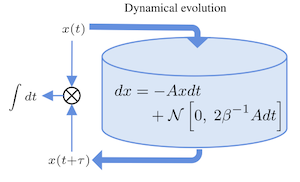
Common algorithms for computationally simulating Langevin dynamics must discretize the stochastic differential equations of motion. These resulting finite-time-step integrators necessarily have several practical issues in common: Microscopic reversibility is violated, the sampled stationary distribution differs from the desired equilibrium distribution, and the work accumulated in nonequilibrium simulations is not directly usable in estimators based on nonequilibrium work theorems. Here, we show that, even with a time-independent Hamiltonian, finite-time-step Langevin integrators can be thought of as a driven, nonequilibrium physical process. Once an appropriate work like quantity is defined - here called the shadow work - more recently developed nonequilibrium fluctuation theorems can be used to measure or correct for the errors introduced by the use of finite time steps. In particular, we demonstrate that amending estimators based on nonequilibrium work theorems to include this shadow work removes the time-step-dependent error from estimates of free energies. We also quantify, for the first time, the magnitude of deviations between the sampled stationary distribution and the desired equilibrium distribution for equilibrium Langevin simulations of solvated systems of varying sizes. While these deviations can be large, they can be eliminated altogether by Metropolization or greatly diminished by small reductions in the time step. Through this connection with driven processes, further developments in nonequilibrium fluctuation theorems can provide additional analytical tools for dealing with errors in finite-time-step integrators.