Presentation: NeurIPS 2023 (New Orleans) Physics Colloquium: Thermodynamic AI and Thermodynamic Linear Algebra
Abstract
 Many Artificial Intelligence (AI) algorithms are inspired by physics and employ
stochastic fluctuations, such as generative diffusion models, Bayesian neural 6
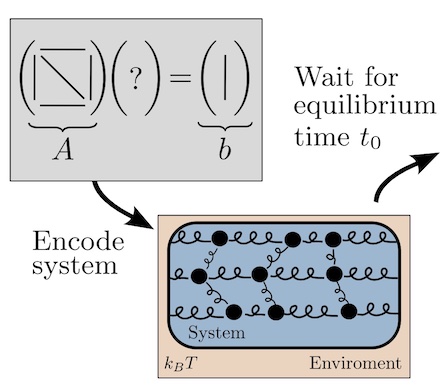
networks, and Monte Carlo inference. These algorithms are currently run on digital hardware, ultimately limiting their scalability and overall potential. Here, we propose a novel computing device, called Thermodynamic AI hardware, that could accelerate such algorithms. Thermodynamic AI hardware can be viewed as a novel form of computing, since it uses novel fundamental building blocks, called stochastic units (s-units), which naturally evolve over time via stochastic trajectories. In addition to these s-units, Thermodynamic AI hardware employs a Maxwell’s demon device that guides the system to
B. Gaussian sampling
produce non-trivial states. We provide a few simple physical architectures for
building these devices, such as RC electrical circuits. Moreover, we show that this same hardware can be used to accelerate various linear algebra primitives.
We present simple thermodynamic algorithms for (1) solving linear systems of equations, (2) computing matrix inverses, (3) computing matrix determinants, and (4) solving Lyapunov equations.
Many Artificial Intelligence (AI) algorithms are inspired by physics and employ
stochastic fluctuations, such as generative diffusion models, Bayesian neural 6
networks, and Monte Carlo inference. These algorithms are currently run on digital hardware, ultimately limiting their scalability and overall potential. Here, we propose a novel computing device, called Thermodynamic AI hardware, that could accelerate such algorithms. Thermodynamic AI hardware can be viewed as a novel form of computing, since it uses novel fundamental building blocks, called stochastic units (s-units), which naturally evolve over time via stochastic trajectories. In addition to these s-units, Thermodynamic AI hardware employs a Maxwell’s demon device that guides the system to
B. Gaussian sampling
produce non-trivial states. We provide a few simple physical architectures for
building these devices, such as RC electrical circuits. Moreover, we show that this same hardware can be used to accelerate various linear algebra primitives.
We present simple thermodynamic algorithms for (1) solving linear systems of equations, (2) computing matrix inverses, (3) computing matrix determinants, and (4) solving Lyapunov equations.