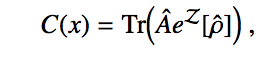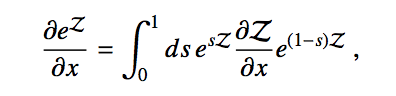Article: Measuring Analytic Gradients of General Quantum Evolution with the Stochastic Parameter Shift Rule
Leonardo Banchi and Gavin E. Crooks, Quantum 5 356 (2021) [ Full text | arXiv Perspective ]
The Parameter Shift Rule is a cunning, recently developed method for evaluation gradients of quantum circuits on a quantum computer. But it has two problems. The first is aesthetic: The derivation has always felt somewhat convoluted to me, although I did my best to explain why the PSR works in a previous paper. The second issues is that the PSR isn’t universal. It only works for certain gates with a special mathematical structure. Again, in a previous paper I described one approach to circumvent that limitation, but that approach itself has limitations.
Last November I was invited to QHACK’19, a quantum hackathon hosted by Xanadu AI. I gave a short talk on gate decompositions and the Parameter Shift Rule, and there met Leonardo Banchi, who also gave a talk on related subjects. Over the next couple of days we fell to chatting, and the collaboration leading to the current paper was born. Leonardo had two key insights. The first was that we should derive the PSR starting from the superoperator formalism of quantum mechanics.
The standard Dirac notation with bra’s and ket’s and unitaries is fine for describing pure quantum dynamics followed by a single measurement. But for anything more complicated than that the Dirac formalism gets really tricky really quickly. Instead we should use density matrices and describe the dynamics with superoperators. Even if the dynamics is still pure and not noisy, superoperators can still provide a simpler representation. This step makes the derivation of the PSR feel much more natural to me.
The second trick is the following operator identity, which is due to Wilcox in the 1960’s.
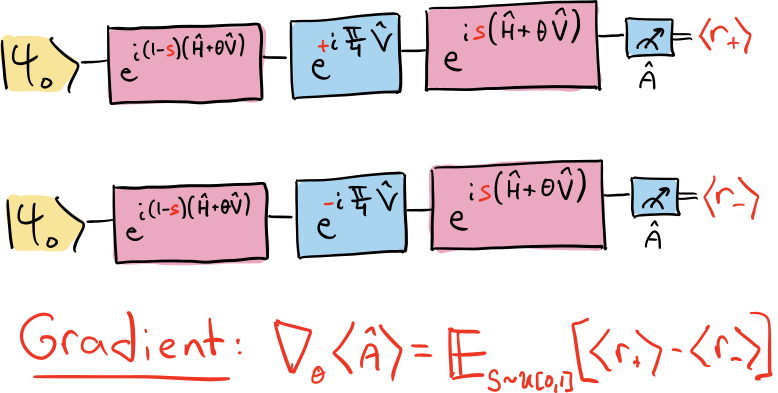
Taking derivatives of exponentials of functions is easy standard calculus. But life gets harder if you want to take derivatives of exponentials of operators. This Wilcox identity neatly solved that problem. Putting this math together with the superoperator description of the dynamics, and we get a general expression for evaluating gradients of quantum gates, which we have called the Stochastic Parameter Shift Rule.
For the technical details, please see our paper. But for a introductory operational overview, take a look at this great PennyLane tutorial from the folks at Xanadu AI, and this perspective Gradients just got more flexible by Johannes Jakob Meyer .
Abstract
Hybrid quantum-classical optimization algorithms represent one of the most promising application for near-term quantum computers. In these algorithms the goal is to optimize an observable quantity with respect to some classical parameters, using feedback from measurements performed on the quantum device. Here we study the problem of estimating the gradient of the function to be optimized directly from quantum measurements, generalizing and simplifying some approaches present in the literature, such as the so-called parameter-shift rule. We derive a mathematically exact formula that provides a stochastic algorithm for estimating the gradient of any multi-qubit parametric quantum evolution, without the introduction of ancillary qubits or the use of Hamiltonian simulation techniques. Our algorithm continues to work, although with some approximations, even when all the available quantum gates are noisy, for instance due to the coupling between the quantum device and an unknown environment.