Article: Thermodynamic matrix exponentials and thermodynamic parallelism
Samuel Duffield, Maxwell Aifer, Gavin Crooks, Thomas Ahle, Patrick J. Coles
Phys. Rev. Res
Abstract
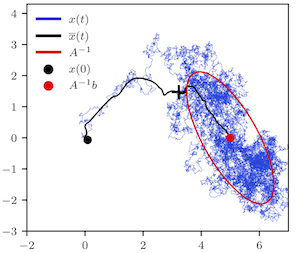
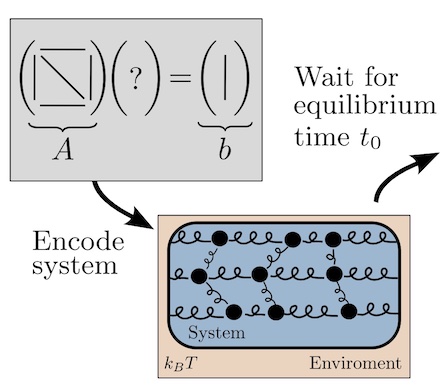
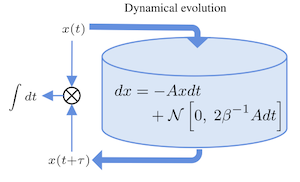Thermodynamic computing exploits fluctuations and dissipation in physical systems to efficiently solve various mathematical problems. It was recently shown that certain linear algebra problems can be solved thermodynamically, leading to a speedup scaling with the matrix dimension. Here, we provide a thermodynamic algorithm for exponentiating a real matrix. We describe a simple electrical circuit involving coupled oscillators, which can implement our algorithm. We also show that this algorithm provides an asymptotic speedup that is linear in the dimension. Finally, we introduce the concept of thermodynamic parallelism to explain this speedup, stating that thermodynamic noise provides a resource leading to effective parallelization of computations.
