Article: Measures of trajectory ensemble disparity in nonequilibrium statistical dynamics
Gavin E. Crooks, and David A. Sivak, J. Stat. Mech.: Theor. Exp. P06003 (2011)
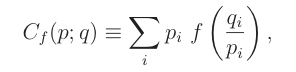
I’ve been meaning to look at the physical significance of f-divergences for some time. These are a class of information type measures that, thanks to the quirks of nonequilibrium thermodynamics, can actually be experimentally measured in real systems. I was finally inspired to write this up due to John Baez, who recently discussed the significance of Rényi entropy to equilibrium statistical mechanics.
Abstract
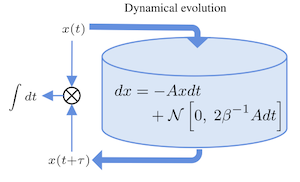
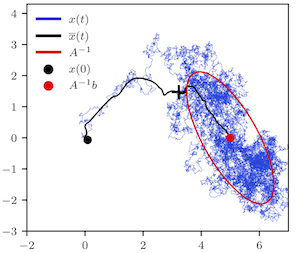
Many interesting divergence measures between conjugate ensembles of nonequilibrium trajectories can be experimentally determined from the work distribution of the process. Herein, we review the statistical and physical significance of several of these measures, in particular the relative entropy (dissipation), Jeffreys divergence (hysteresis), Jensen–Shannon divergence (time-asymmetry), Chernoff divergence (work cumulant generating function), and Rényi divergence.