Article: Thermodynamic metrics and optimal paths
David A. Sivak, Gavin E. Crooks, Phys. Rev. Lett., 108, 190602 (2012)
[ Full Text | Journal | arXiv ]
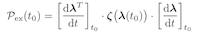
Abstract A fundamental problem in modern thermodynamics is how a molecular-scale machine performs useful work, while operating away from thermal equilibrium without excessive dissipation. To this end, we derive a friction tensor that induces a Riemannian manifold on the space of thermodynamic states. Within the linear-response regime, this metric structure controls the dissipation of finite-time transformations, and bestows optimal protocols with many useful properties. We discuss the connection to the existing thermodynamic length formalism, and demonstrate the utility of this metric by solving for optimal control parameter protocols in a simple nonequilibrium model.