Article: The geometry of thermodynamic control
 Patrick R. Zulkowski
David A. Sivak,
Gavin E. Crooks,
Michael R. DeWeese
Phys. Rev. E, 86, 041148 (2012)
Patrick R. Zulkowski
David A. Sivak,
Gavin E. Crooks,
Michael R. DeWeese
Phys. Rev. E, 86, 041148 (2012)
[ Full text | Journal| arXiv ]
Abstract
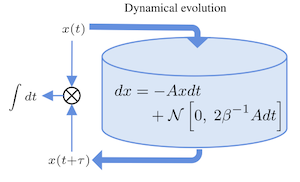
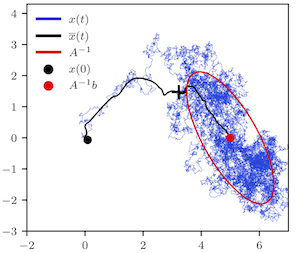
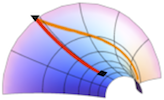
A deeper understanding of nonequilibrium phenomena is needed to reveal the principles governing natural and synthetic molecular machines. Recent work has shown that when a thermodynamic system is driven from equilibrium then, in the linear response regime, the space of controllable parameters has a Riemannian geometry induced by a generalized friction tensor. more We exploit this geometric insight to construct closed-form expressions for minimal-dissipation protocols for a particle diffusing in a one dimensional harmonic potential, where the spring constant, inverse temperature, and trap location are adjusted simultaneously. These optimal protocols are geodesics on the Riemannian manifold, and reveal that this simple model has a surprisingly rich geometry. We test these optimal protocols via a novel numerical implementation of the Fokker-Planck equation and demonstrate that the friction tensor arises naturally from a first order expansion in temporal derivatives of the control parameters, without appealing directly to linear response theory.